This post is a continuation of my previous Blog.
Subtractive mixing and inks
Let's start with subtractive mixing and inks. Unlike what we discussed in the previous blog, pigments in paint interact/mix subtractively. The simplest model to explain how pigments behave is that they remove color (by absorbing particular wavelengths) from the incident light which is then reflected. So the red ink is actually a dye that absorbs green and blue light, therefore the mixing is subtractive. CMY space applies to this subtractive mixing as Cyan can be thought of as White - Red (W-R), Magenta as White - Green (W-G) and Yellow as White - Blue (W-B). Now we can evaluate the mixture from an RGB space reference. For example Cyan and Magenta when mixed give (W-R) + (W-G) = R + G + B - R - G = B (W = R+G+B). Most of the printing devices use atleast four inks (Cyan, Magenta, Yellow and Black) as mixing colors leads to a poor black (Also color inks are generally more expensive than black ; and few other reasons which I don't understand myself such as "it is difficult to ensure good enough registration between the three color inks to avoid colored haloes around text", feel free to explain it in the comments.)
Non-Linear Color Spaces
The coordinates of a color in a linear color space might not encode properties that are common in language or are important in applications.Some terms which are commonly used are hue , property of color that changes from red to green; saturation, property of color that changes from red to pink; brightness, property of color that changes from white to black. It also seems (from intuition) that hues form a circle, in the sense that hue changes from red through orange to yellow, and then green, and from there to cyan, blue, purple, and then red again. This means that no linear color space can model hue as the color coordinate with a maximum value will be very far away from the one with the minimum value.
Playing with RGB color cube :)
HSV space is just viewing RGB cube from another angle and assigning the new coordinates from that view so that we can incorporate the terms what we mentioned above.
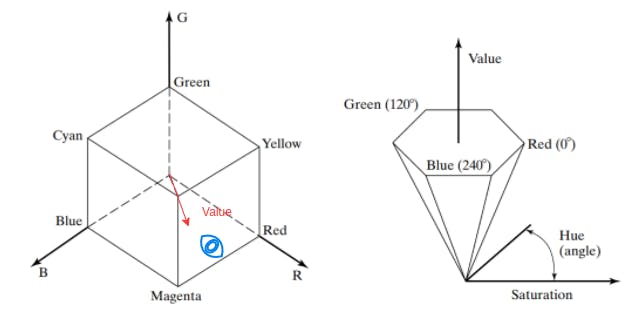 Viewing RGB cube from the neutral axis (origin to (1,1,1)) to see hexagon
Viewing RGB cube from the neutral axis (origin to (1,1,1)) to see hexagon
Uniform Color Spaces
Its very difficult to reproduce colors exactly, which leads to how much difference in color will be noticeable to a viewer. One can modify the colors slightly and ask a viewer to tell when he/she notices change. When these collection of colors which are almost indistinguishable to a viewer are plotted on a CIE xy color space (discussed in the first series of blog), ellipses are formed which are called MacAdam ellipses. If the color space was uniform, these boundaries would have been circles. So a uniform color space is one in which the distance between two coordinates (representing two colors) is a fair representation of difference between two colors. So a uniform color space can be made from CIE xy by using a projective transformation to skew ellipses to circles, yielding uniform color spaces such as CIE u'v', CIE LAB.
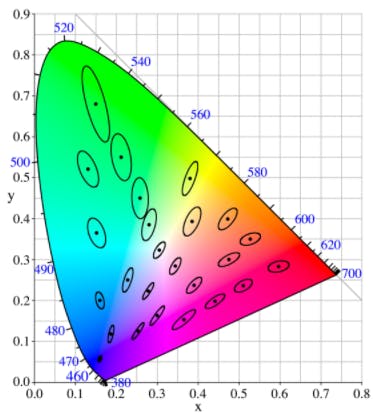 MacAdam ellipses
MacAdam ellipses
In the next series of this blog, I will discuss point operators, linear filtering, non linear filtering, transformations etc. Feel free to point any mistake or if you can add something to it :)

