Colors: Property of perception, not inherent in the object

Both biological and artificial receptors respond differently to different wavelengths. This response captures some information that is perceived by the brain as color.

Color space is a dense forest, one might dedicate his life to exploring the jungle of colors :) To start with, we will briefly skim the color-matching experiment. In this, we have a fixed number of primaries in the mixture whose intensity we vary. A human sees a colored light ie test light in one half and the other half is the resultant of the mixture of the primaries. The intensity is changed until there's a color match. T is for the test light, w_i non-negative weight, P_i the corresponding primaries

T = w₁P₁ + w₂P₂....

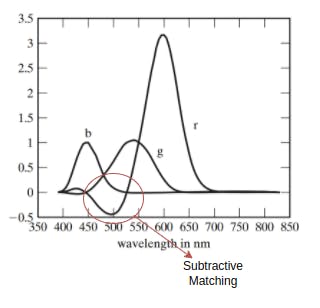
But one will observe that a lot of test colors can't be matched. This is solved if we allow subtractive matching ie allowing weights to be negative which translates into the experiment as adding one of the primaries to the test light and then matching the test light with the mixture in the other half. It is observed that most of the observers require only three primaries to match the mixture with the test light. This phenomenon is known as the principle of trichromacy. However, there are some caveats. Subtractive matching is allowed, primaries must be independent ie no mixture of the primaries should match third. There are strong evidences now that principle of trichromacy holds because there are three distinct (long-wavelength, medium-wavelength, short-wavelength) types of color transducers in the eye. Principle of univariance states that the activity of the these transducers is one kind ie they respond strongly or weakly, but do not some information encoding the wavelength of the light falling on them. Matching (up to an accurate approximation) is linear. Thus, Grassman's laws are yielded.If we mix two test lights, then mixing the mixture of matches will match the result that is if

T_a = w_a1P₁ + w_a2P₂ + w_a3P₃ and T_b = w_b1P₁ + w_b2P₂ + w_b3P₃

then

T_a + T_b = (w_a1+w_b1)P₁ + (w_a2+w_b2)P₂ + (w_a3+w_b3)P₃

also, if two test lights can be matched with the same set of weights, then they will match each other. That is

T_a = w₁P₁ + w₂P₂ + w₃P₃

and

T_b = w₁P₁ + w₂P₂ + w₃P₃

then T_a = T_b

Finally, matching is linear if:

T_a = w₁P₁ + w₂P₂ + w₃P₃

then

kT_a = kw₁P₁ + kw₂P₂ + kw₃P₃

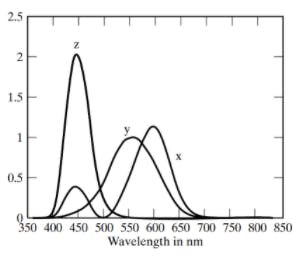
Color matching functions for primaries for the RGB system. Credits

Color Spaces If we take RGB as primaries, then an RGB color space is made by mapping R,G,B onto a 3-D cartesian coordinate system. This results in a 3-D cube where black is (0.0, 0.0, 0.0), and white is (1.0, 1.0, 1.0).

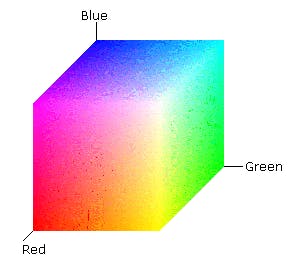RGB color space Credits

But we have troubling fact that if the primaries are real lights, at least one of the color matching functions is negative for some wavelengths. One way to avoid this problem is to tweak color matching functions that are everywhere positive (then we will have imaginary primaries). In such an attempt CIE XYZ color space was born. The color matching functions were chosen to be everywhere positive, so that the coordinates of any real light are always positive.

Credits

Linear color spaces allows various graphical constructions that are more difficult to draw in 3D, so we intersect the XYZ space with the plane X+Y+Z = 1 as shown below

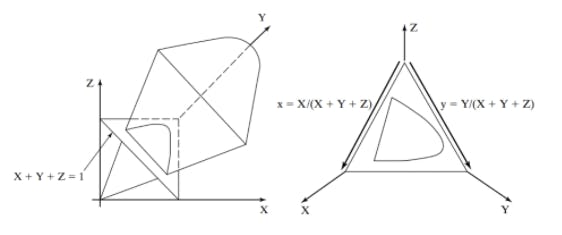(Taken from Computer Vision A modern approach book)

Inks, non-linear color space, MacAdam ellipses etc in the upcoming blogs. Feel free to point out mistakes or suggestions (I am a noob yet ;p)