Brief Linear Algebra Review

Vector Space: We define vector space as a set of all elements that are closed under vector addition and scalar multiplication operations. (closed means that after some operation on vector you will again get vector)

Norm: Norm is a function that takes vector and returns non-negative number. It satisfies following properties:

• Positivity: ||x|| >= 0
• Definiteness: ||x|| = 0 if and only if x = 0
• Absolutely homogenous: ||alpha . x|| |alpha|||x||
• Triangle inequality: ||x+y|| <= ||x|| + ||y||

L2 or Euclidean norm:

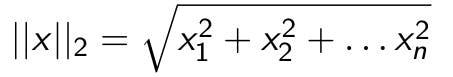
L1 or Manhattan norm:

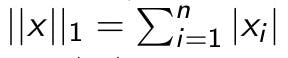
Infinity norm:

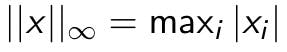
P-norm:

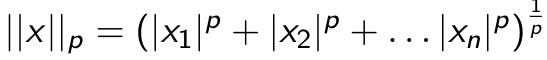
Inner Product: Inner product is a function that takes two vectors from vector space and returns a real number. Functions need to satisfy following properties:

• Positivity: >= 0
• Definiteness: = 0 if and only if x = 0
• Additivity: = + < y,z>
• Homogeneity: = lambda
• Symmetry: =

Inner product and norm can be related to each other as follows: ||x|| = sqrt()

Linear Independence Given vectors v1, v2, ….. vn are said to be linearly independent if no vector can be written as a linear combination of other vectors. We can form a vector space V from a given set of vectors by taking linear combinations.

Span All linear combinations of elements

Basis A set B of vectors in a vector space V is called a basis if every element of V may be written in a unique way as a finite linear combination of elements of B. (In short it is Linear independence + Span)

Dimension Cardinality of basis

Matrix multiplication is

• Not commutative
• associative (AB)C = A(BC)
• Distributive A(B+C) = AB + AC

Transpose of a Matrix

B = A^T

B_ij = A_ij

• (A^T)^T = A
• (A+B)^T = A^T + B^T
• (AB)^T = B^TA^T

Trace of a matrix

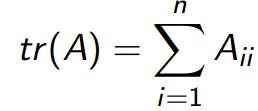
Properties:

• tr(A) = tr(A^T
• tr(A+B) = tr(A) + tr(B)
• tr(AB) = tr(BA)

Inverse of a square matrix AA^-1 = A^-1 A = I

Properties:

• (A^-1)^-1 = A
• (AB)^-1 = B^-1A^-1
• (A^-1)^T = (A^T)^-1

Row rank and Column rank

• Size of the largest subset of rows/ columns of A that constitute a linearly independent set.
• Row rank = Column rank

Properties:

• rank(A) = rank(A^T
• rank(A+B) <= rank(A) + rank(B)
• rank(AB) <= min(rank(A), rank(B))

Inverse doesn’t exist when A is not full rank.

Range is the span of columns of A Nullspace is the the set of vectors when multiplied by A give a zero vector. Orthonormal matrix** Columns are orthogonal to one another and each column is normalized. U^TU = I = UU^T

• Symmetric Matrix, A = A^T
• Anti-Symmetric Matrix, A = -A^T
• Frobenius Norm:
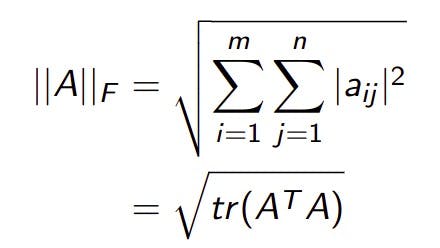
• Kronecker product

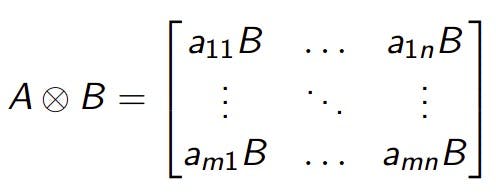
Eigen Values and Eigen Vectors A non zero vector x is called eigen vector if it satisfies: Ax = \(\lambda\)x , where \(\lambda\) is called eigenvalue of matrix A.

Properties:

• tr(A) = \(\sum_{i=1}^{n} \lambda_i\)
• det(A) = \(\prod_{i=1}^{n} \lambda_i\)